为了讨论直升机的动力学问题,先对直升机的类别进行简介。按照旋翼的数目与配置以及叶片数目来区分,直升机有如下几种:
单旋翼直升机
顾名思义,单旋翼直升机就是它只有一个旋翼。一般它必须带一个尾桨负责抵消旋翼产生的反转矩。例如,欧洲直升机公司制造的EC-135直升机。

图1就是一个带尾桨的单旋翼直升机图片。
但是,也有单旋翼直升机无尾桨的情况,这时它的机身尾部侧面有空气排出管道,用喷气的反作用力来抵消旋翼产生的反转矩。例如,美国麦道直升机公司生产的MD520N直升机。“旋翼产生的反转矩”将是本文的讨论的重点。
双旋翼直升机
双旋翼直升机具有两个旋翼。两个旋翼的排列有如下三个情况:
纵列式:两个旋翼前后纵向排列,旋转方向相反。例如,美国波音公司制造的CH-47“支努干”运输直升机。
横列式:两个旋翼左右横向排列,旋翼轴间隔较远,旋转方向相反。比如,前苏联的Mi-12直升机。
共轴式:两个旋翼上下排列,在同一个转轴线上,互成反向旋转。例如,前苏联的卡-50武装直升机。(请见图7的共轴式双旋翼直升机图片)
四旋翼直升机

图2是中国研制的四旋翼无人直升机。四个旋翼分为两对,分别以正螺旋和反螺旋方向旋转。
叶片数量
叶片数量往往与载重量大小相关,常见有2,3,4,8 个叶片。例如米-8直升机有4个叶片;米-28有5个叶片;米-26直升机的旋翼有8个叶片,尾桨有5个叶片。2008年5月26日,一架红色米-26直升机吊装了一台重约13.2吨的重型挖掘机,前往唐家山堰塞湖坝体。图3为执行该项任务的米-26直升机照片。

图3丨 “米-26”直升机
倾转式旋翼飞机
美国V-22鱼鹰直升机就是倾转式旋翼飞机(参见图4),它兼有直升机和飞机的共同优点。当旋翼的转轴竖直时,旋翼产生升力。当转轴角(与竖直轴的夹角)接近90度时,旋翼就变成螺旋桨,飞行速度由300公里/时,提高到500公里/时。现在,美国V-22部署到东亚美军驻日基地,对中国进行威慑。

图4丨V-22“鱼鹰”倾斜(倾转)式旋翼飞机
直升机旋翼动力学奥妙与动量矩守恒律
前边提到,单旋翼直升机除了有一个大的旋翼外,在尾部还有一个小的尾旋翼(也叫尾桨)。图5是一个带镶嵌式尾旋翼(尾桨)的直升机。尾桨产生的作用力沿水平方向,并且与机身垂直,对机身重心有一个力矩(转矩)。再仔细看,尾桨力矩使机身转动的方向必然和主旋翼的转动方向相反。在设计时,要保证尾桨的转矩与旋翼的动量矩大小相等方向相反。这样直升机才能正常飞行。下面我们从力学原理出发来讨论一下直升机运行的奥秘。

图5丨带镶嵌式尾桨的直升机
动量矩定理 (Theorem of moment of momentum) 和动量矩守恒定律 (Law of conservation of moment of momentum) 是刚体(或质点系)运动必须满足的动力学原理。动量矩定理说,动量矩对时间的变化率等于外加力矩之总和。当质点系不受外力作用或所受全部外力对某定点或定轴的主矩始终等于零时,该质点系对该点或该轴的动量矩保持不变。即当作用于它的外力矩之和为零时,它的动量矩变化率将等于零。这就是动量矩守恒定律。
为了更严格地说明动量矩定理和动量矩守恒定律,请看下边的公式:
动量矩
质点对某点的动量矩为L0(mv)= rmv; 其中,黑体符号L0、 r、v都是向量。这个公式表明,质点m对0点的动量矩L0等于质点m到0点的矢径r与其动量mv的矢量积。
刚体的动量矩为Lz=Jzω; 其中,Jz为刚体对于转轴的转动惯量,ω是角速度向量。
动量矩定理
动量矩对时间的变化率等于外加力矩之总和,就是:
[Lz]' =∑Mz(Fi )
其中,等号左边是对动量矩Lz求时间导数,右边是对外力矩求和。
动量矩守恒定律
当上式的右端项为零时,Lz为常数,即动量矩永恒不变。直升机在空中飞行时,它的旋翼不停地旋转,这将产生对直升机重心的动量矩。由于它是孤立系统,外界对它的外力矩之和为零,如果没有尾桨的话,机身将不停地向旋翼旋转的反向旋转,这样就难以执行所指定的各类任务。安装尾桨就是要以尾桨的力矩平衡这个“旋翼产生的反转矩”。这就是直升机安装尾桨的力学意义。
为使机身不产生旋转,也不安装尾桨。聪明的工程师们设计了共轴式双旋翼直升机(参见图6)。它的两幅旋翼安装在同一个轴上,分别朝不同方向旋转,二者的动量矩必须大小相等,构成平衡。若是双轴两旋翼情况(如V-22鱼鹰直升机),要求两个旋翼的转动方向相反且动量矩相等。对于四轴四旋翼情况,很容易推断,它们要两两成对,分别朝反向转动,动量矩大小要相等,以保证总动量矩为零。

图6丨共轴式双旋翼直升机
刚体的转动惯量
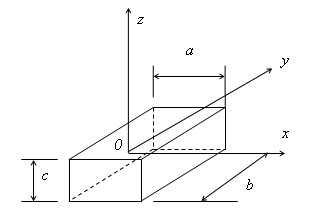
上节提到Jz为刚体对转轴的转动惯量,它和物体平动的惯性量(即质量)类似。当转动惯量越大时,转动它越困难,或者使它转动角速度增大越困难。具有相同质量的物体,形状不同,其转动惯量大小不同。以图7所示实心长方体为例。这是一个三维尺寸为aⅹbⅹc的长方体,为简单起见,令b=2a=4c;根据理论力学教科书,有如下公式:
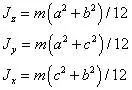
其中:Jz,Jy,Jx分别是绕z,y,x三个轴、对物体重心点0的转动惯量。可见,Jz最大,Jx次之,Jy最小。
刚体的转动惯量问题,和我们身边的许多活动息息相关,这里以竞技运动为例。体操和跳水运动员在做空翻或翻腾动作时,其身体的姿势(形态)决定了其动作的难度,裁判打分时给不同的难度系数。例如图8a 所示的跳水女运动员所做的团身空翻(或向后翻腾),她的身体曲折成三段,各部分身体重量最靠近于重心。于是,其转动惯量最小,可以使翻腾速度最快。所以,在10米台跳水做翻腾三周半的动作时都多采用团身翻腾。图8b所示的则是曲体空翻(或向后翻腾),她的身体呈曲两段折叠,其转动惯量比团身情况稍大。难度系也较大。最难做的是图8c所示的体操运动员所做的直体空翻。由于直体的转动惯量最大,空翻最费力;难度系数最大。同时由于姿态优美,打分较高。

图8a丨团身空翻

图8b(左) 丨曲体空翻 图8c(右)丨 直体空翻
另外,与转动惯量有关的例子还有高空走钢丝。图9是阿迪力在新疆喀纳斯高空走钢丝的照片。你看他两手紧握一根很长的平衡杆。这根平衡杆与他的身体紧紧结合为一体,总的转动惯量大大增加。一个很大转动惯量的物体,是不易被转动的,所以他的直立状态较为稳定,比较安全。相反,如果没有这个平衡杆,他茕茕一身走在钢丝上,就很易翻倒。这就是走钢丝的人必须握有平衡杆的力学奥秘。

图9丨阿迪力新疆喀纳斯高空走钢丝
最后,和动量矩守恒有关的例子是陀螺仪,它是具有高速旋转刚体转子、服从动量矩守恒律的一种常用仪表。现代高精度的单自由度陀螺常是液浮、磁浮和气浮并用的三浮陀螺仪。这种陀螺仪的精度极高。陀螺仪广泛应用于各种运载体(如船舶、飞机等)上,成为各种运载体的自动控制、制导和导航系统中测定姿态、方位的重要元件。
华越无人机教育是广东省首家无人机教育培训机构,是华南区无人机驾驶证考试中心,无人机教员培训中心,是广东省规模最大、课程设置最完整的无人机培训学校。同时也是直升机黄埔军校,80%的直升机飞手都毕业于华越无人机教育。

最新开班信息:
3月 1 日 脱产53班开班
3月15日 脱产54班开班
3月4日无人机飞控知识技术讲座
扫一扫,关注我们 ↓
